เอกนาม (Monomial) คือ นิพนธ์ที่เป็นผลคูณระหว่างตัวเลขหรือค่าคงที่และตัวแปรตั้งแต่ 1 ตัวขึ้นไปและกำลังของแต่ละตัวแปรนั้นไม่น้อยกว่า 0 (มากกว่า หรือ เท่ากับ 0) ซึ่งอยู่ในรูปแบบ
เอกนาม = ค่าคงตัว (ตัวเลขใดๆ) x ตัวแปร (ที่มีเลขชี้กำลังเป็น 0 หรือจำนวนเต็มบวก)
ตัวอย่าง 3x อ่านว่า สามเอ็กซ์ หมายถึง 3×x
-5y อ่านว่า ลบห้าวาย หมายถึง -5×y
xy อ่านว่า เอ็กซ์วาย หมายถึง x×y
x2y อ่านว่า เอ็กซ์กำลังสองวาย หมายถึง x×x×y
xy2z3 อ่านว่า เอ็กซ์วายกำลังสองแซดกำลังสาม หมายถึง x×y×y×z×z×z
0.6ab4 อ่านว่า ศูนย์จุดหกเอบีกำลังสี่ หมายถึง 0.6×a×b×b×b×b
-5y อ่านว่า ลบห้าวาย หมายถึง -5×y
xy อ่านว่า เอ็กซ์วาย หมายถึง x×y
x2y อ่านว่า เอ็กซ์กำลังสองวาย หมายถึง x×x×y
xy2z3 อ่านว่า เอ็กซ์วายกำลังสองแซดกำลังสาม หมายถึง x×y×y×z×z×z
0.6ab4 อ่านว่า ศูนย์จุดหกเอบีกำลังสี่ หมายถึง 0.6×a×b×b×b×b
หมายเหตุ
1) นิพจน์ (Expression) คือ ข้อความในรูปสัญลักษณ์ เช่น 8, 9a, -4x + 7, a +2b – 3 ฯลฯ
2) 5 เป็นเอกนามตัวด้วย เพราะเราเขียน 5 ในรูปที่มีตัวแปรได้ คือ 5×0 (x0 = 1)
2) 5 เป็นเอกนามตัวด้วย เพราะเราเขียน 5 ในรูปที่มีตัวแปรได้ คือ 5×0 (x0 = 1)
3) นิพนธ์ที่ไม่เป็นเอกนาม เช่น
xy-3 ไม่เป็นเอกนามเพราะ y มีกำลังติดลบ
xy-3 ไม่เป็นเอกนามเพราะ y มีกำลังติดลบ
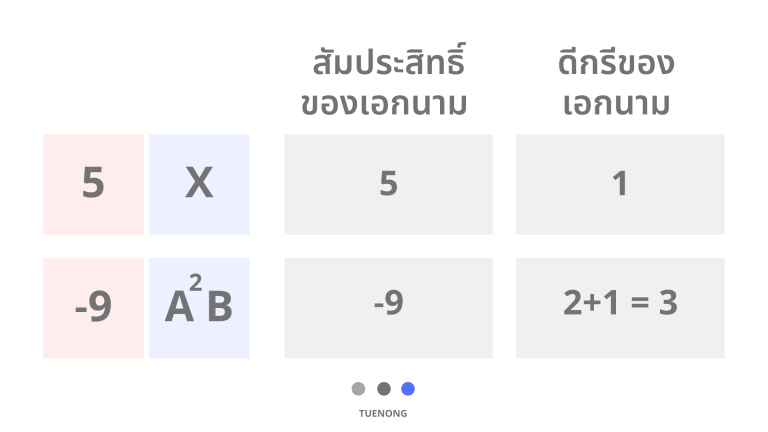
4) สัมประสิทธิ์ของเอกนาม คือ ค่าคงที่ที่อยู่หน้าตัวแปร
5) ดีกรีของเอกนาม คือ ผลบวกของเลขชี้กำลังทั้งหมดตัวของแปร
6) a = 1×a (ตัวแปรใดที่ไม่เห็นตัวเลข ให้คิดว่ามี 1 คูณอยู่ด้านหน้า)
7) x = x1 (ตัวแปรใดที่ไม่เห็นกำลัง ให้คิดว่ามีกำลังเท่ากับ 1)
5) ดีกรีของเอกนาม คือ ผลบวกของเลขชี้กำลังทั้งหมดตัวของแปร
6) a = 1×a (ตัวแปรใดที่ไม่เห็นตัวเลข ให้คิดว่ามี 1 คูณอยู่ด้านหน้า)
7) x = x1 (ตัวแปรใดที่ไม่เห็นกำลัง ให้คิดว่ามีกำลังเท่ากับ 1)
ตัวอย่าง
|
เอกนาม
|
สัมประสิทธิ์
|
ดีกรี
|
|
3
|
3
|
0 (มาจาก3x0)
|
|
5x
|
5
|
1 (มาจาก5x1)
|
|
-y2
|
-1
|
2
|
|
3xy
|
3
|
2 (1+1)
|
|
4x2y
|
4
|
3 (2+1)
|
|
0.5ab3
|
0.5
|
4 (1+3)
|
|
-6a4b2
|
-6
|
6 (4+2)
|
|
11a3bc5
|
11
|
9 (3+1+5)
|
เอกนามคล้าย คือ เอกนามที่มีตัวแปรชุดเดียวกัน และเลขชี้กำลังของตัวแปรเดียวกันในแต่ละเอกนามเท่ากัน
ตัวอย่าง
ตัวอย่าง
| 2xy คล้ายกับ 7xy -7xy2 คล้ายกับ xy2 4x3y คล้ายกับ –x3y xy คล้ายกับ yx abc คล้ายกับ cba |
2ab5 คล้ายกับ -2ab5 6a3b2c คล้ายกับ 9a3cb2 xy ไม่คล้ายกับ xy2 3xyz2 ไม่คล้ายกับ 3xy2z 3a2 ไม่คล้ายกับ 3b2 |
ไฟล์ตัวอย่าง