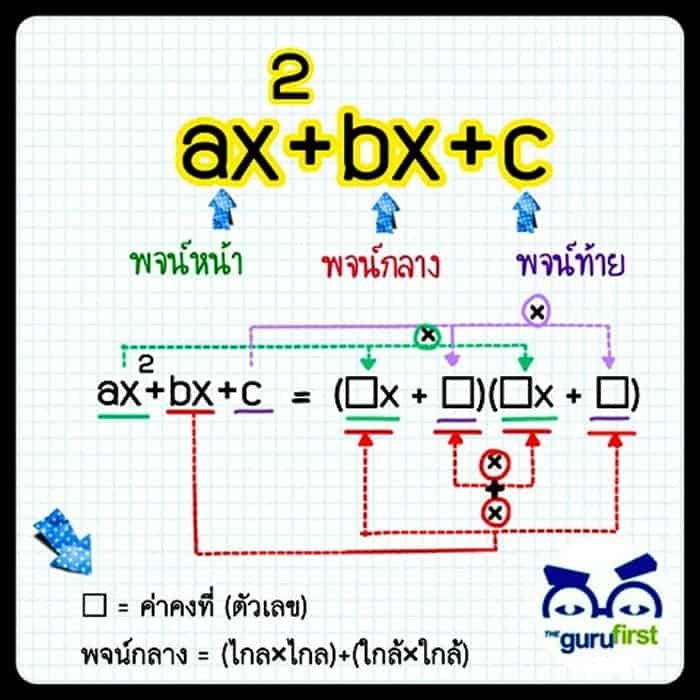
พหุนามดีกรีสองตัวแปรเดียว คือ พหุนามที่เขียนได้ในรูป ax2 + bx + c เมื่อ a, b, c เป็นค่าคงตัว ที่ a ≠ 0 และ x เป็นตัวแปร เพื่อความสะดวกในการหาข้อสรุปของวิธีแยกตัวประกอบของหพุนาม ax2 + bx + c จะเรียก ax2 ว่า พจน์หน้า เรียก bx ว่า พจน์กลาง และเรียก c ว่า พจน์หลัง ซึ่งการแยกสามารถทำได้ดังนี้
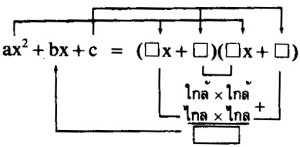 ตัวอย่างเช่น จงแยกตัวประกอบของ 5x2 – 11x + 2
ตัวอย่างเช่น จงแยกตัวประกอบของ 5x2 – 11x + 2
ขั้นที่ 1 …แยกพจน์หน้าเป็นสองพจน์ ได้ 5x กับ x
……………………………..(5x ……..)(x……..)
ขั้นที่ 2 …แยกพจน์ท้ายออกเป็นสองจำนวนคูณกัน ได้ (-2)×(-1) นำไปใส่ในขั้นตอนที่ 1 สามารถใส่ได้ 2 แบบ คือ
……………………………..(5x – 2)(x – 1) กับ (5x – 1)(x – 2)
ขั้นที่ 3 …หาพจน์กลางจากขั้นตอนที่ 2 โดยนำ (ใกล้ ×ใกล้) + (ไกล ×ไกล) ถ้าได้ผลลัพธ์เป็น -11x แสดงว่าการแยกตัวประกอบนั้นถูกต้อง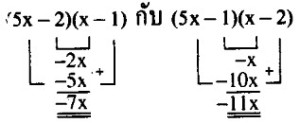 ……………. ดังนั้น 5x2 – 11x + 2 = (5x – 1)(x – 2) ตอบ
……………. ดังนั้น 5x2 – 11x + 2 = (5x – 1)(x – 2) ตอบ