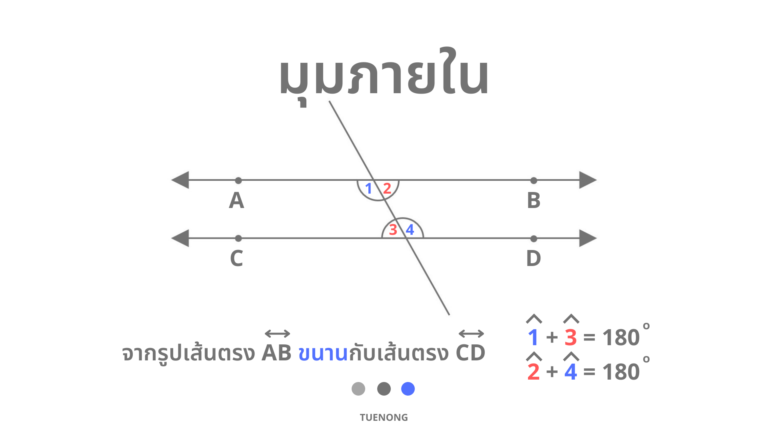
เส้นขนานและมุมภายใน นิยาม เส้นตรงสองเส้นที่บนระนาบเดียวกันขนานกันเมื่อเส้นทั้งสองนี้ไม่ตัดกัน

1. ถ้าเส้นตรงสองเส้นขนานกันและมีเส้นตัดแล้วขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเป็น 180 องศา
2. ถ้าเส้นตรงเส้นหนึ่งตัดเส้นตรงคู่หนึ่ง ทำให้ขนาดของมุมภายในที่อยู่บนข้างเดียวกันของเส้นตัดรวมกันเป็น 180 องศาแล้ว เส้นตรงคู่นี้จะขนานกัน

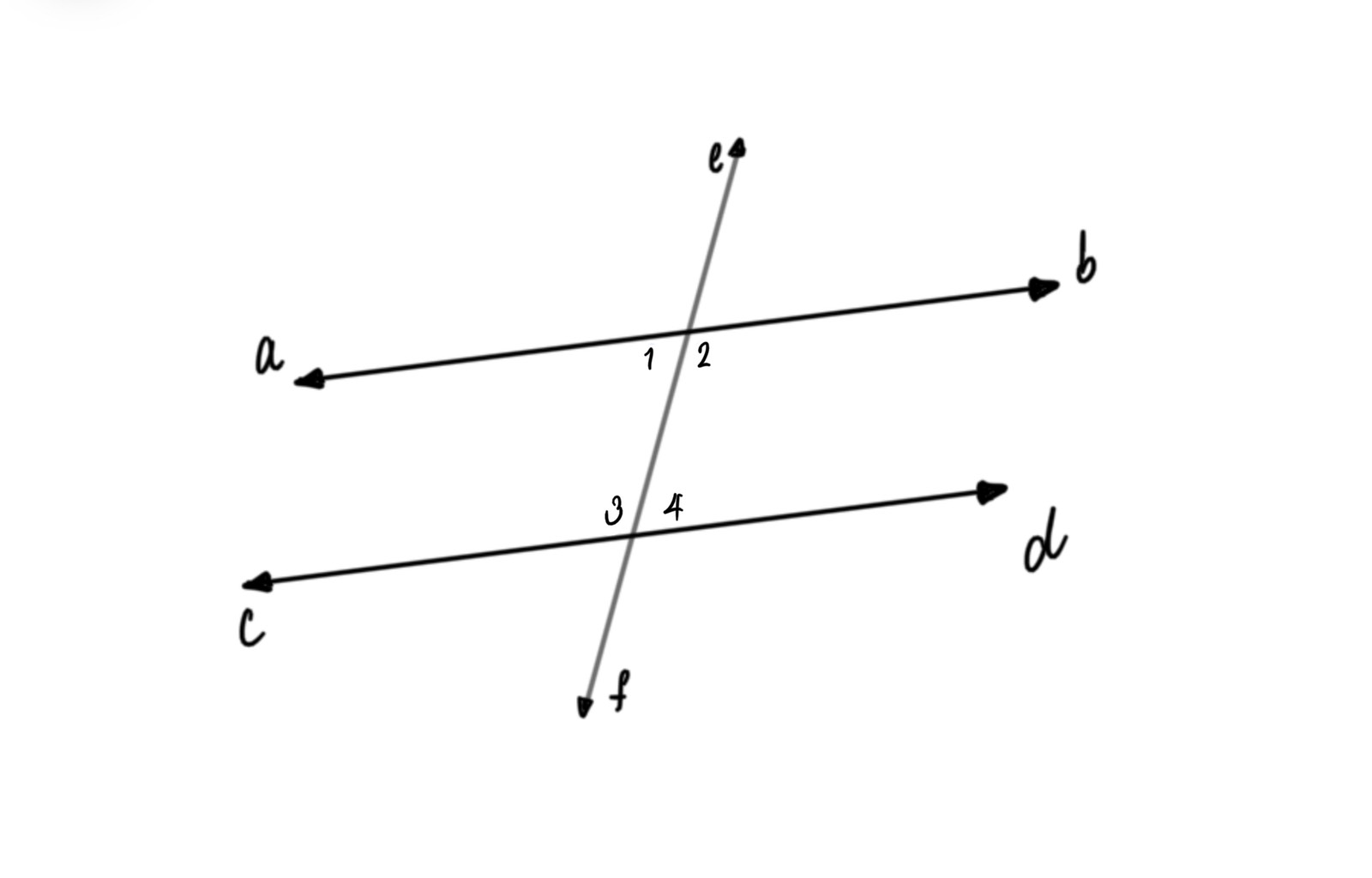
“เส้นตรงสองเส้นขนานกัน และมีเส้นตรงเส้นหนึ่งตัดเราเรียกมุมที่อยู่ภายในระหว่างเส้นคู่ขนานเรียกว่า มุมภายใน”

มุมภายในบนข้างเดียวของเส้นตัด

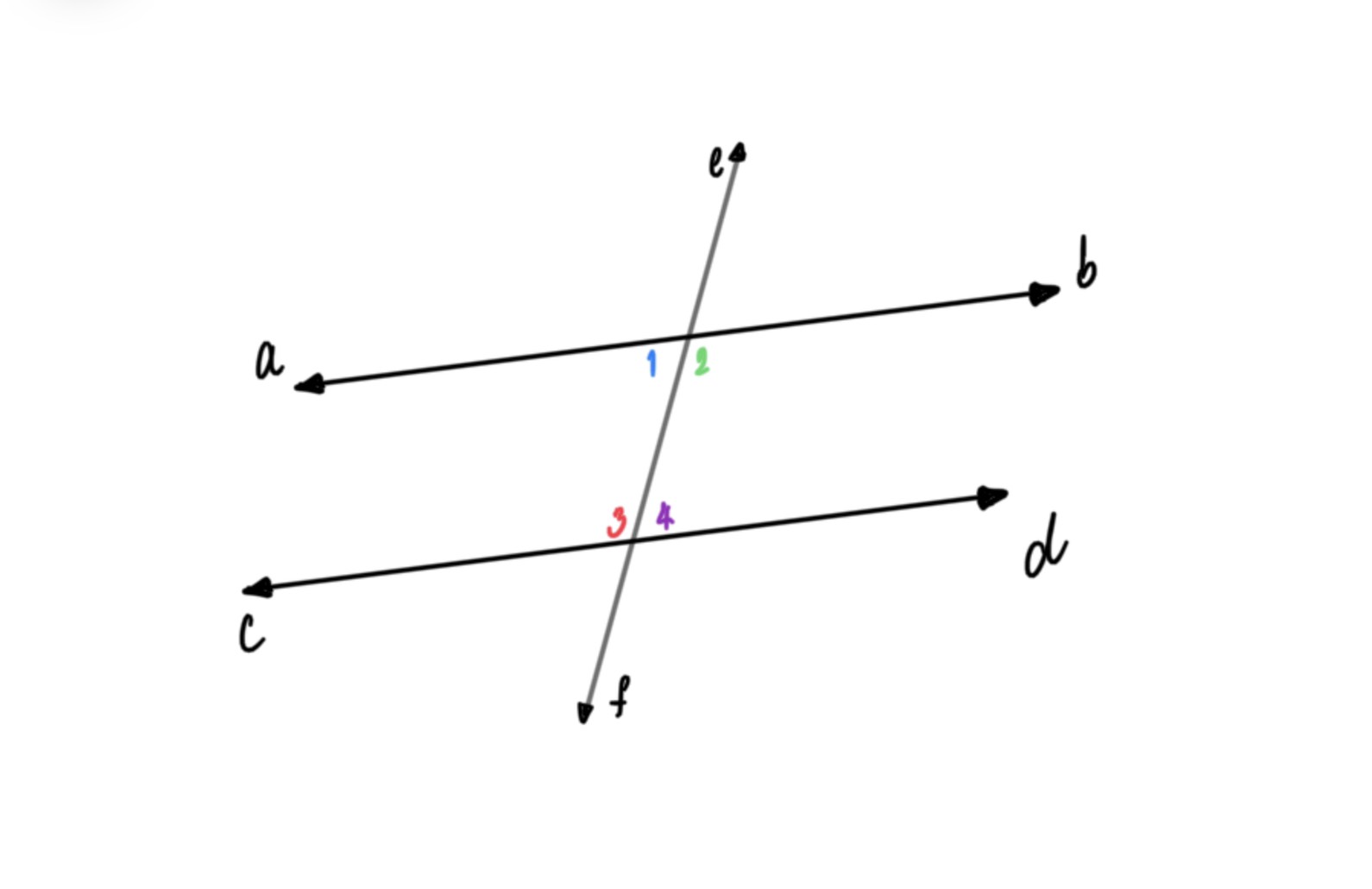
ab // cd มีเส้นตรง ef ตัด ทำให้เกิดมุมภายในบนข้างเดียวกันของเส้นตัดสองข้าง คือ มุม 1 กับ 3 และ มุม 2 กับ 4